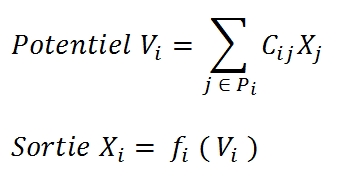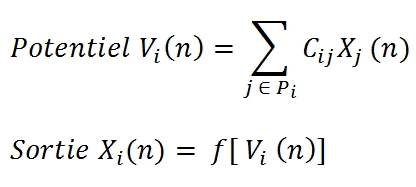Réseaux de neurones 1
Zythom - Blog d'un informaticien expert judiciaire - Zythom, 3/03/2013
Depuis que je me suis mis en tête de reprendre mes travaux de recherches sur les réseaux de neurones (lire le billet "désir de vieux quadra"), j'essaye de voir comment aborder cette question sur ce blog.
Je crois que je vais le faire de la manière la plus simple du monde: en mélangeant les billets avec les autres thèmes abordés ici, dans un joyeux chaos qui me correspond tellement bien.
Les lecteurs qui ne sont pas intéressés pourront rapidement zapper les billets qui seront intitulés "réseaux de neurones N", et ceux éventuellement intéressés pourront s'abonner au flux Rss (ou Atom) de la rubrique "Réseaux de neurones".
Mais je vous préviens tout de suite, je n'ai aucune idée de où cela va mener, ni du temps que je pourrai y consacrer, ni même si j'arriverai à quelque chose. Ce que j'appelle ici "recherche" est un travail personnel que je souhaite partager sur ce blog. Vous y verrez certainement des défauts, des failles et des maladresses que je vous encourage à signaler.
Je rappelle enfin aux nouveaux lecteurs que ce blog est un blog personnel sans prétention mais pour lequel j'ai des principes d'indépendance.
Je suis allé regarder la page Wikipédia consacrée aux réseaux de neurones, et je la trouve très bien faite. Elle constitue une très bonne introduction à ce billet et je vous invite à aller l'étudier.
Les neurones biologiques peuvent être modélisés d'une manière très très simplifiée de la façon suivante:
- un neurone reçoit de l'information de la part d'un certain nombre d'autres neurones. Ces informations seront supposées être de nature principalement électrique. Je noterai ces informations Xi où i sera le numéro du neurone dans le réseau.
- toutes les liaisons entre neurones ne sont pas équivalentes en importance, il est donc judicieux de pondérer l'information électrique avec un coefficient associé à la liaison concernée. Ce coefficient sera noté Cij où i et j sont les numéros respectifs de deux neurones reliés l'un à l'autre dans le réseau.
- le neurone reçoit toutes les informations pondérées et en fait la somme (comme pour un potentiel électrique). Cette somme sera appelée "potentiel du neurone". On le notera Vi.
- un neurone ne peut pas avoir une sortie Xi trop importante, sinon il va "griller". Il faut donc limiter la valeur de Xi par le haut.
- inversement, un neurone ne génèrera un signal d'information Xi que si son potentiel Vi est suffisamment élevé. Il faut donc fixer un seuil d'activation (au dessous duquel le neurone restera inactif).
Toutes ces constations, issues plus ou moins d'observations sur les neurones biologiques, amènent à établir les relations suivantes:
Le potentiel Vi du neurone i = somme des produits ( Cij Xj ) où j parcourt l'ensemble des indices des neurones qui sont reliés au neurone numéro i, où Cij est le poids de la synapse reliant le neurone j au neurone i (on dit également coefficient synaptique) et où Xj est la sortie du neurone j.
La sortie Xi du neurone i = f ( Vi ) où f est une fonction de transformation du potentiel limitant la valeur de la sortie quand Vi est grand et permettant d'avoir une sortie Xi nulle si Vi est trop faible. Cette fonction est appelée fonction d'activation.
Soit, grace à la concision du langage mathématique, pour chaque neurone d'indice i :
où Pi est l'ensemble des indices des neurones envoyant leurs valeurs au neurone i
La fonction d'activation :
Comme indiqué précédemment, cette fonction a pour rôle d'introduire une non linéarité dans le réseau. Elle limite la valeur maximum de la sortie d'un neurone et reste nulle pour des potentiels trop faibles.
La fonction d'activation souvent utilisée est la fonction sigmoïde ou la tangente hyperbolique. Pour ma part, je choisie cette dernière car elle est centrée sur zéro, ce qui permettra d'amorcer plus facilement l'algorithme d'apprentissage, comme nous le verrons plus tard.
En préparant ce billet, je me suis demandé s'il n'était pas plus simple d'utiliser une fonction sinus pour les potentiels compris entre -pi/2 et +pi/2 et deux demie-droites horizontales à -1 et +1 pour le reste. Je n'ai jamais testé, mais cela me semble une idée intéressante pour abréger l'apprentissage (qui dépend des fonctions dérivées). On verra.
Pour simplifier le comportement du futur ensemble de neurones que l'on appellera "réseau de neurones", je fais l'hypothèse que tous les neurones utilisent la même fonction d'activation, ce qui me permet de retirer l'indice "i" sur le "f" des formules précédentes.
J'ai volontairement omis des formules précédentes le fait que les potentiels (et donc les sorties) des neurones vont varier au cours du temps. Vi et Xi sont donc des fonctions du temps. J'aurais du écrire Vi(t) et Xi(t). Mais comme je vais travailler dans un univers discrétisé, je préfère écrire Vi(n) et Xi(n).
Nous aurons donc comme modèle pour un neurone i à un instant n :
où Pi est l'ensemble des indices des neurones envoyant leurs valeurs au neurone i.
Un schéma est peut-être plus explicite :
La mise en réseau :
Un réseau de neurones de ce type est un ensemble de neurones reliés les uns aux autres de façon à ce que l'information puisse circuler sans boucle pour que tous les potentiels soient calculables à un instant n.
En outre, afin de relier le réseau au monde extérieur, le réseau dispose de capteurs d'entrée qui seront considérés comme des sorties de neurones imposées par le monde extérieur.
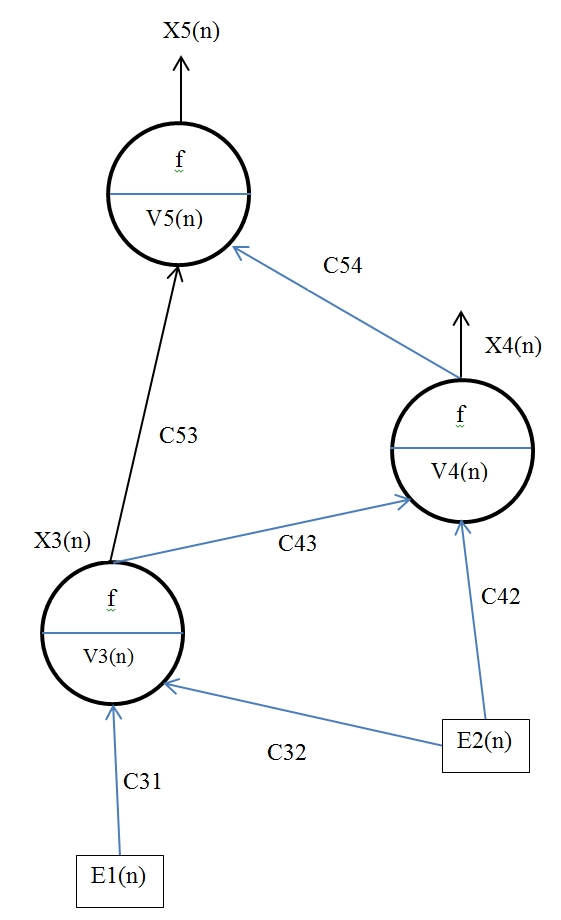
Voici un exemple de réseau de 3 neurones avec deux entrées :
Le monde extérieur impose le comportement des neurones d'entrée E1 et E2.
J'ai choisi de mesurer les sorties des deux neurones X4 et X5.
La sortie du neurone numéro 3 est interne au réseau.
Tous les choix faits ici sont pour l'instant arbitraires (nombre d'entrées, nombre de neurones, architecture des connexions, sorties sélectionnées...).
Il est important de comprendre que les six coefficients Cij de ce réseau sont les inconnues à calculer si l'on souhaite que le réseau ait un comportement particulier pour un ensemble de stimuli imposés.
Nous verrons tous cela dans un autre billet.
Pour l'instant, j'ai beaucoup de choses à apprendre sur le langage Go que Stéphane Bortzmeyer m'a fait découvrir sur Twitter, et cela va me prendre beaucoup de temps... Ça parle de parallélisme, de passage de messages sur des canaux, toutes choses prometteuses pour mes futures simulations. Mais je ne dois pas oublier qu'il va aussi me falloir mettre en place mes routines d'optimisation favorites...
Je me sens l'âme d'un étudiant (et j'aime ça ;-).
Je crois que je vais le faire de la manière la plus simple du monde: en mélangeant les billets avec les autres thèmes abordés ici, dans un joyeux chaos qui me correspond tellement bien.
Les lecteurs qui ne sont pas intéressés pourront rapidement zapper les billets qui seront intitulés "réseaux de neurones N", et ceux éventuellement intéressés pourront s'abonner au flux Rss (ou Atom) de la rubrique "Réseaux de neurones".
Mais je vous préviens tout de suite, je n'ai aucune idée de où cela va mener, ni du temps que je pourrai y consacrer, ni même si j'arriverai à quelque chose. Ce que j'appelle ici "recherche" est un travail personnel que je souhaite partager sur ce blog. Vous y verrez certainement des défauts, des failles et des maladresses que je vous encourage à signaler.
Je rappelle enfin aux nouveaux lecteurs que ce blog est un blog personnel sans prétention mais pour lequel j'ai des principes d'indépendance.
Je suis allé regarder la page Wikipédia consacrée aux réseaux de neurones, et je la trouve très bien faite. Elle constitue une très bonne introduction à ce billet et je vous invite à aller l'étudier.
Les neurones biologiques peuvent être modélisés d'une manière très très simplifiée de la façon suivante:
- un neurone reçoit de l'information de la part d'un certain nombre d'autres neurones. Ces informations seront supposées être de nature principalement électrique. Je noterai ces informations Xi où i sera le numéro du neurone dans le réseau.
- toutes les liaisons entre neurones ne sont pas équivalentes en importance, il est donc judicieux de pondérer l'information électrique avec un coefficient associé à la liaison concernée. Ce coefficient sera noté Cij où i et j sont les numéros respectifs de deux neurones reliés l'un à l'autre dans le réseau.
- le neurone reçoit toutes les informations pondérées et en fait la somme (comme pour un potentiel électrique). Cette somme sera appelée "potentiel du neurone". On le notera Vi.
- un neurone ne peut pas avoir une sortie Xi trop importante, sinon il va "griller". Il faut donc limiter la valeur de Xi par le haut.
- inversement, un neurone ne génèrera un signal d'information Xi que si son potentiel Vi est suffisamment élevé. Il faut donc fixer un seuil d'activation (au dessous duquel le neurone restera inactif).
Toutes ces constations, issues plus ou moins d'observations sur les neurones biologiques, amènent à établir les relations suivantes:
Le potentiel Vi du neurone i = somme des produits ( Cij Xj ) où j parcourt l'ensemble des indices des neurones qui sont reliés au neurone numéro i, où Cij est le poids de la synapse reliant le neurone j au neurone i (on dit également coefficient synaptique) et où Xj est la sortie du neurone j.
La sortie Xi du neurone i = f ( Vi ) où f est une fonction de transformation du potentiel limitant la valeur de la sortie quand Vi est grand et permettant d'avoir une sortie Xi nulle si Vi est trop faible. Cette fonction est appelée fonction d'activation.
Soit, grace à la concision du langage mathématique, pour chaque neurone d'indice i :
où Pi est l'ensemble des indices des neurones envoyant leurs valeurs au neurone i
La fonction d'activation :
Comme indiqué précédemment, cette fonction a pour rôle d'introduire une non linéarité dans le réseau. Elle limite la valeur maximum de la sortie d'un neurone et reste nulle pour des potentiels trop faibles.
La fonction d'activation souvent utilisée est la fonction sigmoïde ou la tangente hyperbolique. Pour ma part, je choisie cette dernière car elle est centrée sur zéro, ce qui permettra d'amorcer plus facilement l'algorithme d'apprentissage, comme nous le verrons plus tard.
Fonction tangente hyperbolique - Image source Wikipédia
En préparant ce billet, je me suis demandé s'il n'était pas plus simple d'utiliser une fonction sinus pour les potentiels compris entre -pi/2 et +pi/2 et deux demie-droites horizontales à -1 et +1 pour le reste. Je n'ai jamais testé, mais cela me semble une idée intéressante pour abréger l'apprentissage (qui dépend des fonctions dérivées). On verra.
Pour simplifier le comportement du futur ensemble de neurones que l'on appellera "réseau de neurones", je fais l'hypothèse que tous les neurones utilisent la même fonction d'activation, ce qui me permet de retirer l'indice "i" sur le "f" des formules précédentes.
J'ai volontairement omis des formules précédentes le fait que les potentiels (et donc les sorties) des neurones vont varier au cours du temps. Vi et Xi sont donc des fonctions du temps. J'aurais du écrire Vi(t) et Xi(t). Mais comme je vais travailler dans un univers discrétisé, je préfère écrire Vi(n) et Xi(n).
Nous aurons donc comme modèle pour un neurone i à un instant n :
où Pi est l'ensemble des indices des neurones envoyant leurs valeurs au neurone i.
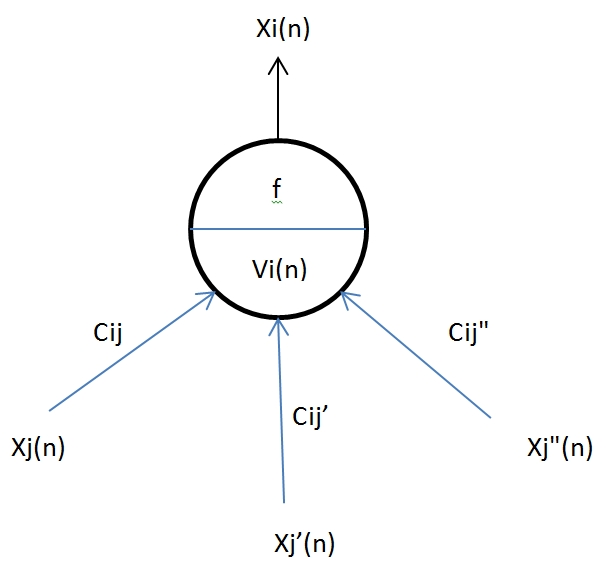
Un schéma est peut-être plus explicite :
Modèle de neurone
La mise en réseau :
Un réseau de neurones de ce type est un ensemble de neurones reliés les uns aux autres de façon à ce que l'information puisse circuler sans boucle pour que tous les potentiels soient calculables à un instant n.
En outre, afin de relier le réseau au monde extérieur, le réseau dispose de capteurs d'entrée qui seront considérés comme des sorties de neurones imposées par le monde extérieur.
Voici un exemple de réseau de 3 neurones avec deux entrées :
Le monde extérieur impose le comportement des neurones d'entrée E1 et E2.
J'ai choisi de mesurer les sorties des deux neurones X4 et X5.
La sortie du neurone numéro 3 est interne au réseau.
Tous les choix faits ici sont pour l'instant arbitraires (nombre d'entrées, nombre de neurones, architecture des connexions, sorties sélectionnées...).
Il est important de comprendre que les six coefficients Cij de ce réseau sont les inconnues à calculer si l'on souhaite que le réseau ait un comportement particulier pour un ensemble de stimuli imposés.
Nous verrons tous cela dans un autre billet.
Pour l'instant, j'ai beaucoup de choses à apprendre sur le langage Go que Stéphane Bortzmeyer m'a fait découvrir sur Twitter, et cela va me prendre beaucoup de temps... Ça parle de parallélisme, de passage de messages sur des canaux, toutes choses prometteuses pour mes futures simulations. Mais je ne dois pas oublier qu'il va aussi me falloir mettre en place mes routines d'optimisation favorites...
Je me sens l'âme d'un étudiant (et j'aime ça ;-).
----------------------------------------------
Source image Megaportail